Let’s lay down some definitions:
- Let FF be a field and let EE be an extension of FF. An element α∈Eα∈E is algebraicover FF if there is a polynomial f(x)f(x) in F[x]F[x] such that f(α)=0f(α)=0 (i.e. α∈Eα∈E is an algebraic element if it is the root of some polynomial with coefficients in FF).
- Let FF be a field and let EE be an extension of FF. If K⊂EK⊂E is a subset of EE which contains all elements which are algebraic over FF, then KK is actually a subfieldof EE and an algebraic extension of FF. We call KK the algebraic closure of FF and denote it by ¯¯¯¯FF¯. [1]
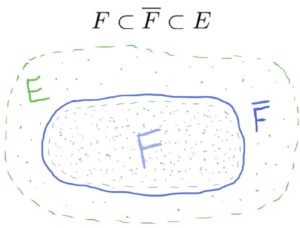
It’s a fact that an algebraic closure ¯¯¯¯FF¯ exists for every field FF (and is actually unique up to isomorphism). So we can draw a containment picture like the one above.
Those familar with some topology and/or analysis will notice that such a “field tower” is suggestive of a vaguely analogous result: given a topological space XX we can always (assuming some conditions about XX, namely it being locally-compact Hausdorff) stick an open set VV and its closure ¯¯¯¯VV¯ between a certain compact set KK and open set UU: K⊂V⊂¯¯¯¯V⊂U.K⊂V⊂V¯⊂U.
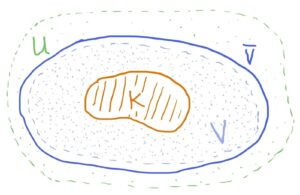
Now, don’t buy too much into the analogy. I only mention this topological result to motivate the fact that the closure of a set and the algebraic closure of a field do indeed convey the same concept: wholeness. It seems then that we can view algebraic elements as the mathematical cousins of limit points of sequences of real numbers. Why? Because, topologically speaking, what is the closure of a set? The collection of limit points of that set, right? So in particular, when we let our topological space be RR, the set of real numbers (with the usual topology) and consider the subset {xn}∞n=1{xn}n=1∞ – some sequence of real numbers,
- we say x∈Rx∈R is a limit pointof {xn}{xn} if for every ϵ>0ϵ>0 there is an n∈Nn∈N such that |xn−x|<ϵ|xn−x|<ϵ.
Then in light of our comments above, we can make the analogous statement for a subset of polynomials {fn(x)}⊂F[x]⊂E[x]{fn(x)}⊂F[x]⊂E[x]:
- We say α∈Eα∈E is an algebraic element(over FF) if there is an n∈Nn∈N such that fn(α)=0fn(α)=0**.
Notice there’s no need for an approximation by ϵϵ in the second bullet. Why? Well, imagine placing a “metric” dd on E[x]E[x] by d:E[x]×E[x]→Ed:E[x]×E[x]→E via***
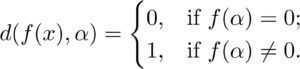
(So intuitively, f(x)f(x) is far away from αα if αα is not a root, but if αα is a root of f(x)f(x), then f(x)f(x) and αα are just as close as they can be.) In this way, the distance between an algebraic element and its corresponding polynomial is precisely 0. So in this case there’s no need to approximate a distance of zero by an arbitrarily small ϵϵ-ball – we have zero exactly!
And thus we have stumbled upon another insight into one of the main differences between analysis and algebra: you know the adage –
Analysts like inequalies; algebraists like equalities!

Digging Deeper
It would be interesting to see if there’s something in the language of category theory which allows one to see that closure of an algebraic field and closure of a topological set really are the same. Now I don’t know much about categories, but as one of my classmates recently suggested, we might want to look for a functor from the category of fields to the category of topological spaces such that the operation of closure is equivalent in each. In this case, perhaps it’s more appropriate to relate an algebraic closure to the completion of a topological space, as opposed to its closure. Admittedly, I’m not sure about all the details, but I think it’s worth looking into!
Footnotes:
* This is actually a bit deceiving. How we measure “closeness” really depends on the topology of the space we’re working on. For example, we can place the ray topology on RR so that the open sets are intervals of the form (a,∞)(a,∞) for a∈Ra∈R. Then in the strict definition of a limit point we see that -763 is a limit point of the interval (0,1)(0,1) even though it’s “far away”!
** Okay okay… there’s no reason to assume an arbitrary collection of polynomials is countable. I really should write FF for some family of polynomials in which case this statement would read “…if there is some f∈Ff∈F such that f(α)=0f(α)=0.” But bear with me for analogy’s sake.
*** I put “metric” in quotes here because as defined dd is not a metric in the strict sense of the word. Indeed, we don’t have the condition d(f(x),α)=0d(f(x),α)=0 if and only if “f(x)=αf(x)=α” since the latter is like comparing apples and oranges! But it would be interesting to see if we could place looser version of a metric on a polynomial ring. For instance, the way I’ve defined dd here, an open ball centered at αα would correspond to all polynomials in E[x]E[x] which have αα as a root! This idea seems to be related to Hilbert’s Nullstellensatz and the Zariski topology.
For more such insights, log into www.international-maths-challenge.com.
*Credit for article given to Tai-Danae Bradley*

