A mathematical game governed by simple rules throws up patterns of seemingly infinite complexity – and now a question that has puzzled hobbyists for decades has a solution.
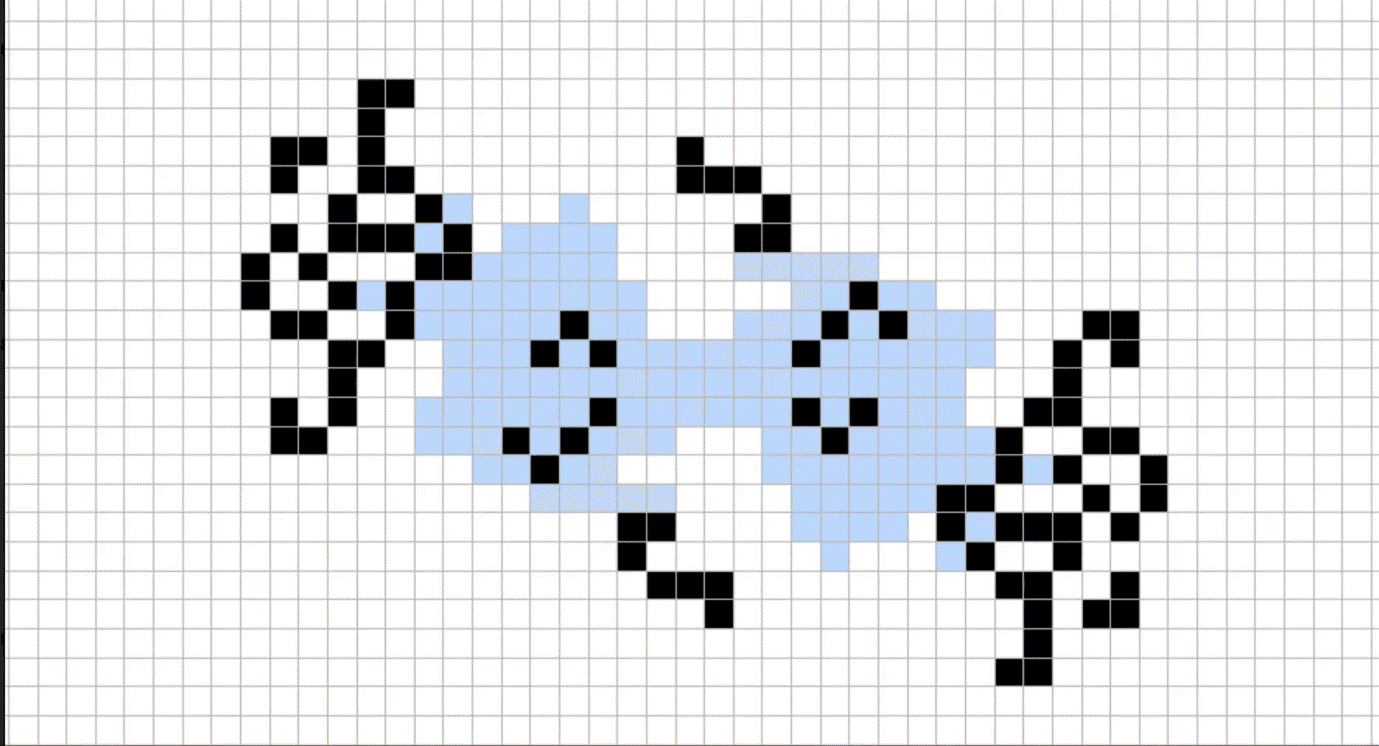
A pattern in the Game of Life that repeats after every 19 steps
A long-standing mystery about repeating patterns in a two-dimensional mathematical game has been solved after more than 50 years with the discovery of two final pieces in the puzzle.
The result is believed to have no practical application whatsoever, but will satisfy the curiosity of the coterie of hobbyists obsessed with the Game of Life.
Invented by mathematician John Conway in 1970, the Game of Life is a cellular automaton – a simplistic world simulation that consists of a grid of “live” cells and “dead” cells. Players create a starting pattern as an input and the pattern is updated generation after generation according to simple rules.
A live cell with fewer than two neighbouring live cells is dead in the next generation; a live cell with two or three neighbouring live cells remains live; and a live cell with more than three neighbouring live cells dies. A dead cell with exactly three neighbouring live cells becomes live in the next generation. Otherwise, it remains dead.
These rules create evolving patterns of seemingly infinite complexity that throw up three types of shape: static objects that don’t change; “oscillators”, which form a repeating but stationary pattern; and “spaceships”, which repeat but also move across the grid.
One of the enduring problems in Game of Life research is whether there are oscillators with every “period”: ones that repeat every two steps, every three steps and so on, to infinity. There was a strong clue that this would be true when mathematician David Buckingham designed a technique that could create oscillators with any period above 57, but there were still missing oscillators for some smaller numbers.
Now, a team of hobbyists has filled those last remaining gaps by publishing a paper that describes oscillators with periods of 19 and 41 – the final missing shapes.
One member of the team, Mitchell Riley at New York University Abu Dhabi, works on the problem as a hobby alongside his research in a quantum computing group. He says there are lots of methods to generate new oscillators, but no way has been found to create them with specific periods, meaning that research in this area is a game of chance. “It’s just like playing darts – we’ve just never hit 19, and we’ve never hit 41,” he says.
Riley had been scouring lists of known shapes that consist of two parts, a hassler and a catalyst. Game of Life enthusiasts coined these terms for static shapes – catalysts – that contain a changing shape inside – a hassler. The interior reacts to the exterior, but leaves it unchanged, and together they form an oscillator of a certain period. Riley’s contribution was writing a computer program to discover potentially useful catalysts.
“The stars have to align,” he says. “You need the reaction in the middle to not destroy the thing on the outside, and the reaction in the middle, just by chance, to return to its original state in one of these new periods.”
Riley says that there are no applications known for this research and that he was drawn to the problem by “pure curiosity”.
Susan Stepney at the University of York, UK, says the work demonstrates some “extremely clever and creative techniques”, but it certainly isn’t the final conclusion of research on Conway’s creation.
“I don’t think work on Game of Life will ever be complete,” says Stepney. “The system is computationally universal, so there is always more behaviour to find, and it is seemingly so simple to describe, but so complex in its behaviour, that it remains fascinating to many.”
For more such insights, log into www.international-maths-challenge.com.
*Credit for article given to Matthew Sparkes*