A centuries-old maths problem asks what shape a circle traces out as it rolls along a line. The answer, dubbed a “cycloid”, turns out to have applications in a variety of scientific fields.
Light reflecting off the round rim creates a mathematically significant shape in this coffee cup
Sarah Hart
The artist Paul Klee famously described drawing as “taking a line for a walk” – but why stop there? Mathematicians have been wondering for five centuries what happens when you take circles and other curves for a walk. Let me tell you about this fascinating story…

A wheel rolling along a road will trace out a series of arches
Imagine a wheel rolling along a road – or, more mathematically, a circle rolling along a line. If you follow the path of a point on that circle, it traces out a series of arches. What exactly is their shape? The first person to give the question serious thought seems to have been Galileo Galilei, who gave the arch-like curve a name – the cycloid. He was fascinated by cycloids, and part of their intriguing mystery was that it seemed impossible to answer the most basic questions we ask about a curve – how long is it and what area does it contain? In this case, what’s the area between the straight line and the arch? Galileo even constructed a cycloid on a sheet of metal, so he could weigh it to get an estimate of the area, but he never managed to solve the problem mathematically.
Within a few years, it seemed like every mathematician in Europe was obsessed with the cycloid. Pierre de Fermat, René Descartes, Marin Mersenne, Isaac Newton and Gottfried Wilhelm Leibniz all studied it. It even brought Blaise Pascal back to mathematics, after he had sworn off it in favour of theology. One night, he had a terrible toothache and, to distract himself from the pain, decided to think about cycloids. It worked – the toothache miraculously disappeared, and naturally Pascal concluded that God must approve of him doing mathematics. He never gave it up again. The statue of Pascal in the Louvre Museum in Paris even shows him with a diagram of a cycloid. The curve became so well known, in fact, that it made its way into several classic works of literature – it gets name-checked in Gulliver’s Travels, Tristram Shandy and Moby-Dick.
The question of the cycloid’s area was first solved in the mid-17th century by Gilles de Roberval, and the answer turned out to be delightfully simple – exactly three times the area of the rolling circle. The first person to determine the length of the cycloid was Christopher Wren, who was an extremely good mathematician, though I hear he also dabbled in architecture. It’s another beautifully simple formula: the length is exactly four times the diameter of the generating circle. The beguiling cycloid was so appealing to mathematicians that it was nicknamed “the Helen of Geometry”.
But its beauty wasn’t the only reason for the name. It was responsible for many bitter arguments. When mathematician Evangelista Torricelli independently found the area under the cycloid, Roberval accused him of stealing his work. “Team Roberval” even claimed that Torricelli had died of shame after being unmasked as a plagiarist (though the typhoid he had at the time may have been a contributing factor). Descartes dismissed Fermat’s work on the cycloid as “ridiculous gibberish”. And in response to a challenge from Johann Bernoulli, Isaac Newton grumpily complained about being “teased by foreigners about mathematics”.
An amazing property of the cycloid was discovered by Christiaan Huygens, who designed the first pendulum clock. Pendulums are good for timekeeping because the period of their motion – the time taken for one full swing of the pendulum – is constant, no matter what the angle of release. But in fact, that’s only approximately true – the period does vary slightly. Huygens wondered if he could do better. The end of a pendulum string moves along the arc of a circle, but is there a curved path it could follow so that the bob would reach the bottom of the curve in the same time no matter where it was released? This became known as the “tautochrone problem”. And guess which curve is the solution? An added bonus is its link to the “brachistochrone problem” of finding the curve between any two points along which a particle moving under gravity will descend in the shortest time. There’s no reason at all to think that the same curve could answer both problems, but it does. The solution is the cycloid. It’s a delightful surprise to find it cropping up in situations seemingly so unrelated to where we first encountered it.
When you roll a circle along a line, you get a cycloid. But what happens when you roll a line along a circle? This is an instance of a curve called an involute. To make one, you take a point at the end of a line segment and roll that line along the curve so it’s always just touching it (in other words, it’s a tangent). The involute is the curve traced out by that point. For the involute of a circle, imagine unspooling a thread from a cotton reel and following the end of the thread as it moves. The result is a spiralling curve emerging from the circle’s circumference.
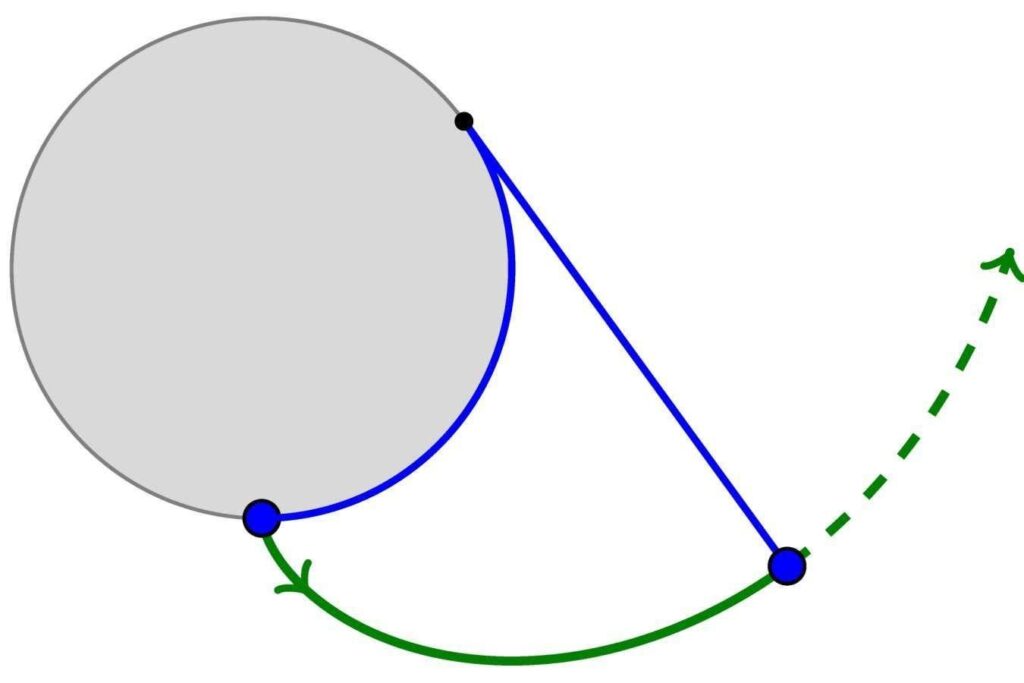
When a line rolls along a circle, it produces a curve called an involute
Huygens was the first person to ask about involutes, as part of his attempts to make more accurate clocks. It’s all very well knowing the cycloid is the perfect tautochrone, but how do you get your string to follow a cycloidal path? You need to find a curve whose involute is a cycloid. The miraculous cycloid, it turns out, has the beautiful property that it is its own involute! But those lovely spiralling circle involutes turn out to be extremely useful too.
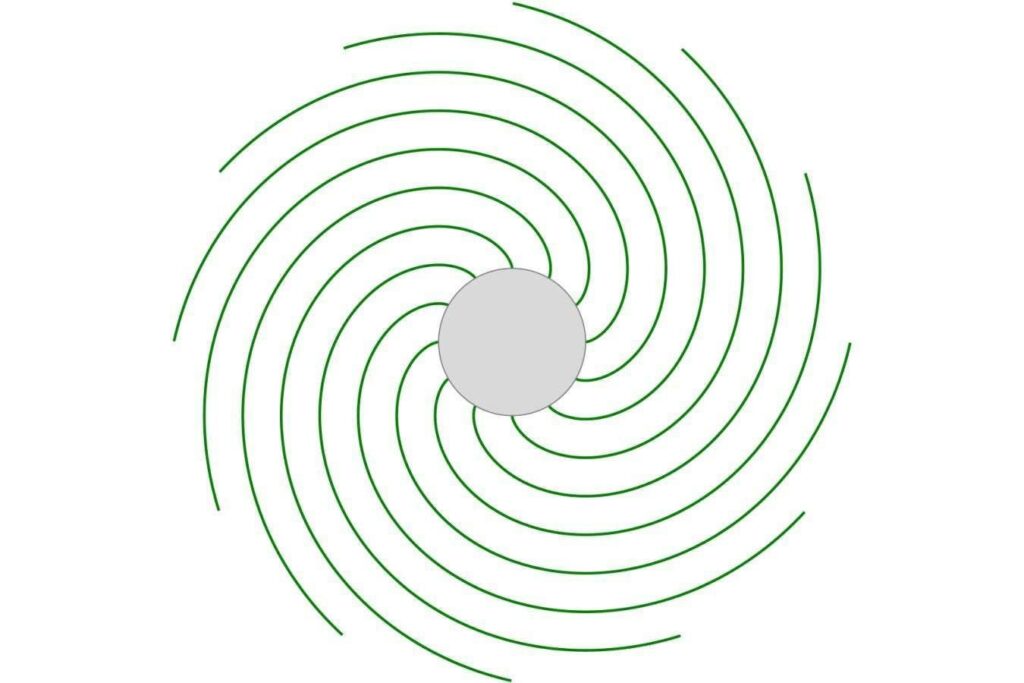
A circle with many involutes
My favourite application is one Huygens definitely couldn’t have predicted: in the design of a nuclear reactor that produces high-mass elements for scientific research. This is done by smashing neutrons at high speed into lighter elements, to create heavier ones. Within the cylindrical reactor cores, the uranium oxide fuel is sandwiched in thin layers between strips of aluminium, which are then curved to fit into the cylindrical shape. The heat produced by a quadrillion neutrons hurtling around every square centimetre is considerable, so coolant runs between these strips. It’s vital that they must be a constant distance apart all the way along their curved surfaces, to prevent hotspots. That’s where a useful property of circle involutes comes in. If you draw a set of circle involutes starting at equally spaced points on the circumference of a circle, then the distances between them remain constant along the whole of each curve. So, they are the perfect choice for the fuel strips in the reactor core. What’s more, the circle involute is the only curve for which this is true! I just love that a curve first studied in the context of pendulum clocks turns out to solve a key design question for nuclear reactors.
We’ve rolled circles along lines and lines along circles. Clearly the next step is to roll circles along circles. What happens? Here, we have some choices. What size is the rolling circle? And are we rolling along the inside or the outside of the stationary one? The curve made by a circle rolling along inside of the circle is called a hypocycloid; rolling it along the outside gives you an epicycloid. If you’ve ever played with a Spirograph toy, you’ll almost have drawn hypocycloids. Because your pen is not quite at the rim of the rolling circle, technically you are creating what are called hypotrochoids.
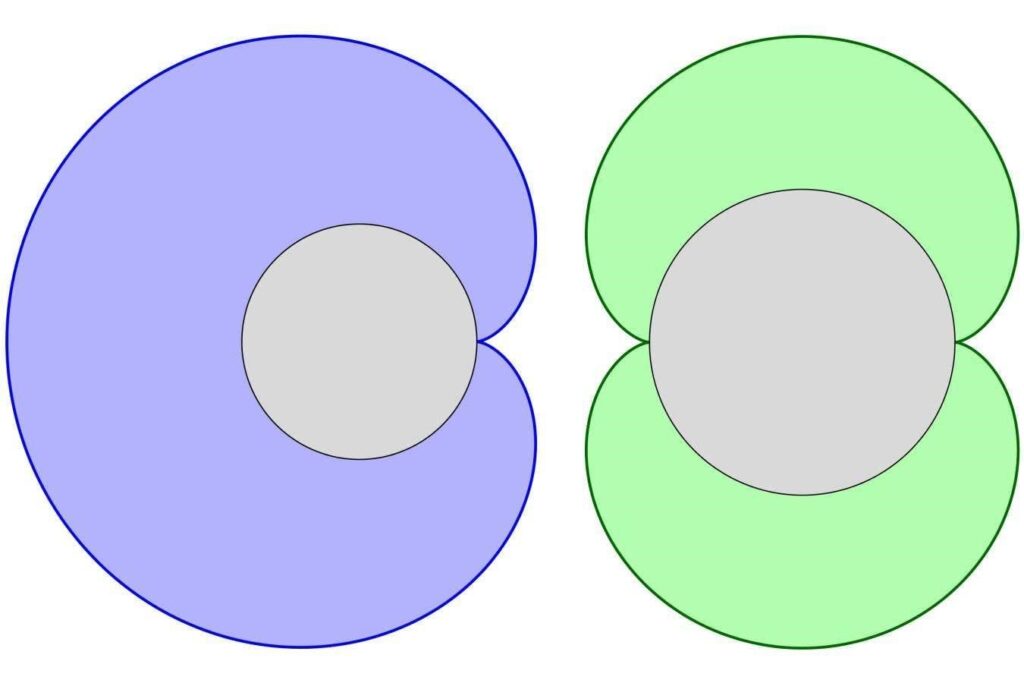
A cardioid (left) and nephroid (right)
Of the epicycloids, the most interesting is the cardioid: the heart-shaped curve resulting when the rolling circle has the same radius as the fixed one. Meanwhile, the kidney-shaped nephroid is produced by a rolling circle half the radius of the fixed one. Cardioids crop up in the most fascinating places. The central region of the Mandelbrot set, a famous fractal, is a cardioid. Sound engineers will be familiar with cardioid microphones, which pick up sound in a cardioid-shaped region. You might also find cardioid-like curves in the light patterns created in coffee cups in some kinds of lighting. If light rays from a fixed source are reflected off a curved mirror, the curve to which each of those reflected rays are tangent will be visible as a concentrated region of light, called a caustic. It turns out that a light source on the circumference of a perfectly circular mirror will result precisely in a cardioid!
Of course, in our coffee cup example, usually the light source isn’t exactly on the rim of the cup, but some way away. If it were very far away, we could assume that the light rays hitting the rim of the cup are parallel. In that situation, it can be shown that the caustic is actually not a cardioid but another epicycloid: the nephroid. Since a strong overhead light is somewhere between these two extremes, the curve we get is usually going to be somewhere between a cardioid and a nephroid. The mathematician Alfréd Rényi once defined a mathematician as “a device for turning coffee into theorems”. That process is nowhere more clearly seen than with our wonderful epicycloids. Check them out if you’re reading this with your morning cuppa!
For more such insights, log into www.international-maths-challenge.com.
*Credit for article given to Sarah Hart*


